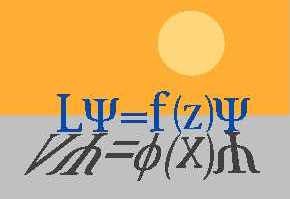Background: Differential operators are linear operators that turn functions into other functions by differentiating and multiplying. They play important roles in math, physics and engineering, but when their product is defined by composition they also form an interesting algebra. For differential operators acting on scalar functions, no differential operator involving differentiation is invertible. Surprisingly, in the case of matrix differential operators, the product of two differential operators of positive order can be the identity. This property seems not to have either been studied or utilized.
Research Problems: There are two questions that we can and should tackle together. One is to understand which matrix differential operators are invertible. That is, we would want some sort of classification theorem. And, once that is achieved, we would be able to use our knowledge of invertible differential operators to produce a new class of operators with the property called bispectrality, a sort of wave-theoretic symmetry that is pictorially represented in this illustration:
What Courses/Skills Do I Need To Have Taken? Math 221 and Math 203 would probably be sufficient background for this project, although additional experience with differential equations and abstract algebra would not hurt.
When Can I Work on the Project? I would be able to work on this in Summer 2016.
Is Funding Available? There has been no grant funding set aside for this project, however there may be grants that we can apply for once we formalize a project.
More Information: Please email Prof. Kasman if you are interested in learning more.