A recent Tweet led me to discover an old blog post written by Christopher Danielson (@Trianglemancsd) back in 2013. His post was titled, “College algebra teachers! Please try this and report back!” Although I don’t teach College Algebra, my current semester includes two sections of our “PreCalculus” course. I tried a modified version of his activity and I’ll describe my version below.
I gave each student a small (roughly 3″x5″) piece of green paper and a small piece of orange paper. I wrote on the board that green meant YES and orange meant NO. Then I passed out a one-page quiz that had six “Yes/No” style questions. The questions were about the function 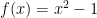 . Each question asked, “Is (number) in the range of the function?” I displayed each question on the projector and then asked the students to vote on the answer by holding their green or orange paper above their head.
. Each question asked, “Is (number) in the range of the function?” I displayed each question on the projector and then asked the students to vote on the answer by holding their green or orange paper above their head.
The first question was, “Is 8 in the range of the function?” In both sections, all of the students answered this question correctly. I asked for a volunteer to explain their reasoning. In the case the reasoning was too short or wasn’t quite right, I asked for another volunteer to explain the answer in a different way.
Next, I asked, “Is -3 in the range of the function?” In both sections, all of the students answered this question correctly. Most explanations cited the fact the graph of the function would show a parabola with a minimum y-value of -1, so -3 was “too low” to be on the parabola.
With the next three questions, most of the students answered correctly and gave appropriate and correct reasoning. The questions asked if 1/4, -1/2, and π were in the range of the function. The last question, though, had an interesting result.
“Is ∞ in the range of the function?”
Every student in both sections of PreCalculus answered “Yes” to this question, at which point I held up an orange paper above my head signaling the answer was “No.” I asked if anyone wanted to change their answers. Lots of people hesitated and looked confused. Then I asked the students for possible reasoning why infinity is not in the range. I tried not to give them any information and instead just ask leading questions — this was hard for me! — but here are some of the comments that were made:
- “Infinity isn’t in the range because it’s so big it has all the negative numbers in it too, and we already said -3 wasn’t in the range.”
- “Infinity isn’t in the range because it’s not a concrete idea.”
- “Infinity isn’t in the range because whenever we write a range using interval notation, we always use open brackets or parentheses for infinity. So this means it’s always less than infinity so infinity doesn’t count.”
- “Infinity isn’t in the range because it’s not a real number.” (Another student then asked, “But π isn’t a real number either because it just goes on and on and on, and we already said it was in the range.” I really think this is an interesting connection! At the end of the activity, I spent a few minutes talking about real numbers and rationals, and how there are plenty of real numbers that aren’t rational and don’t even have patterns in their infinite decimal expansions.)
I thought it was really great to hear everyone’s different ideas of thinking about this question. I was happy that the activity resulted in about a dozen students each talking in class. This was only the second day of our semester, so the students aren’t yet used to each other. Hopefully this activity made them more willing to share ideas and answers during class time.
Thanks to Gregory Taylor and Christopher Danielson for their blog posts about this!
