I’d like to start by pointing out I know nearly nothing about medicine or obstetrics. I wouldn’t call myself an expert in statistics. I am a mathematician: In my life, what this means is that I was trained to approach problems from a very particular viewpoint. When confronted with choices in my own life, I can’t help but think of them as a math professor would. I would love to find someone trained in obstetrics or medicine to collaborate with on the issues I’ve written about below! Do you know of anyone who would be interested?
“The Pregnant Mathematician”
There isn’t a lot written about what it’s like being a pregnant mathematician. While I would guess that the overlap of these two population groups is small, a better reason might be that it is exhausting to be both a mathematician and pregnant at the same time, and the idea of adding “blogger” to that list seems insane.
Nevertheless, it’s difficult for me to think about having either description without the other. I Tweeted yesterday one of my “daydream goals”:
What would I write about? Well, here’s how my pregnancy has become mathematized over the last couple of months.
Glucola for Breakfast
This morning I was screened for Gestational Diabetes (GDM). This required fasting overnight (nothing but water), arriving at the lab, drinking a very sugary drink, waiting an hour, and having my blood drawn. I’m not exactly sure how much I’ll be billed for this test, but my guess is that it will cost about $40 out-of-pocket.
One of the things I’m always interested in is what the false positive rate for these types of screenings is. In other words, if my doctor phones me in a few days and tells me that my screening test came back positive, what is the chance I really have the underlying condition?
During my hour wait in my doctor’s office, I spent some time trying to find out this answer. According to this New Zealand-based maternity site,
“Approximately 15 – 20% of pregnant women test positive on the [glucose screening] test although only 2 – 5% will have any form of diabetes.”
In other words, if we give the same test I took this morning to 100 pregnant women, we should expect 15-20 of them to have a positive result. However, it will turn out (after further screening) that only 2-5 of them will actually have any form of diabetes. So if my OB tells me that today’s screening has come back positive, then this means I am one of the 20 women with positive results; but only 2-5 of us actually have gestational diabetes. Supposing that 5 of us have the condition, that means 5 out of the 20 positives are true positives.
If my screening this morning comes back positive, there’s around a 5/20 = 25% chance I have any form of diabetes. Looking at this another way, without taking the screening test, my “best guess” of my chance of having GDM is between 3% and 10%, based on the incidence rate for the overall population. So I can feel comfortable that there’s between a 90% and 97% chance that I don’t have GDM. But now I have taken the test; if it comes back positive, this means there’s still a 75% chance that I don’t have GDM.
Basically, I think I just paid $40 to find out if my risk is 10%, or if it’s really higher and is 25%.
How valuable is this knowledge? Is it worth fasting overnight? Is it worth taking time off from work to sit in the waiting room for an hour? Is it worth the $40 I’ll be billed? I don’t know. I never know the answers to these questions, but it seems I always choose to follow my OB’s advice anyway — her practice suggests screening of 100% of their maternity patients, so I just trusted their expertise.
Due Date Calculation
One of the things people always ask when they find out you’re pregnant is, “When are you due?” My obstetrician has some date written down on my medical records, labeled EDD (“Expected Date of Delivery”), that will happen this summer. The basic way the EDD is calculated is using Naegele’s Rule: Take the day of your last menstrual period (LMP), add one year, subtract three months, and add seven days. Example: If LMP date was in January this year (say, January 18th, 2013), adding one year gives 1/18/2014, subtracting 3-months gives 10/18/2013, and adding seven days gives a final EDD of October 25, 2013. There are lots of online calculators that will perform this calculation for you, like this one. This calculation gives 280 days post LMP for an estimated delivery date. But how accurate is that?
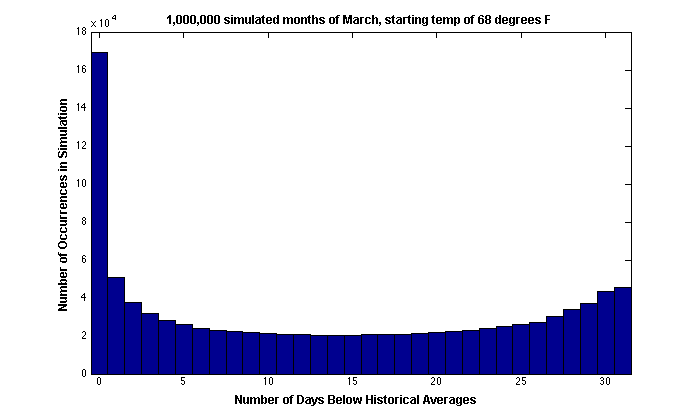
Suppose we take forty weeks (280 days) as the mean length of human pregnancies, measured from LMP to delivery date. It seems reasonable to expect that even if your actual delivery date isn’t your EDD, at least it’ll probably be in the same 7-day window. Unfortunately, this isn’t true either. Not only is it not very likely for you to deliver on your EDD, but it isn’t very likely you’ll deliver that week.
A study done in Norway (Duration of human singleton pregnancy—a population-based study, Bergsjφ P, Denman DW, Hoffman HJ, Meirik O.) involving 427,582 singleton pregnancies found a mean gestation length of 281 days, with a standard deviation of 13 days. By the empirical rule, this means more than 30% of women won’t give birth in the 26-days surrounding their EDD!
Example: Your EDD is June 15th. According to the study cited above, there’s more than a 30% chance that your real delivery day will be either before June 2nd or after June 28th. There’s a very real possibility you won’t even give birth in the month of June. (After talking about this with a few colleagues, one of them found a Statistics book that cited a standard deviation of 16 days!)
Here’s a great article about this same topic: http://spacefem.com/pregnant/charts/duedate0.php
Nuchal Translucency Screening
One non-invasive genetic screening test offered to all pregnant women in the United States is the nuchal translucency screening (“NT screening”). This screening is done in the first trimester (between weeks 11 and 14) and involves an ultrasound and a blood test. It screens for Down Syndrome (trisomy 21) and other chromosomal abnormalities caused by extra copies of chromosomes. The ultrasound image is read by measuring the width of the nuchal fold, found at the base of the neck. If the measurement is outside of the normal range, further testing is indicated. The cost of the test varies widely, but is somewhere in the neighborhood of $200.
The risk of carrying a baby with chromosomal abnormalities increases with maternal age. This page has a large table of the risk of Down Syndrome (and other trisomy abnormalities) as a function of maternal age. I’ll use a maternal age of 29, which carries with it a risk factor of 1 in 1000 for Down Syndrome. This means that out of 1000 moms (all age 29), one will have an affected baby.
One of the problems with the NT screening is the false positive risk. This would happen if your test comes back positive, when in fact you do not have the condition. In other words, this is the “false alarm” risk. According to my OB, the false positive rate for the NT scan is 5%.
Let’s go back and talk about our 1000 women (all pregnant and age 29, with no other risk factors). If we screen all of these women, then a 5% false positive rate means that 5% of them will have a positive test but whose babies do not have Down Syndrome. So that’s 50 women who will get a “false alarm” from this test. Also, one woman will have a true positive: She’ll get a positive test and her baby will have the condition. Altogether, out of the 1000 women, 51 of them will get a positive test. And out of these 51 women, only 1 will have an affected baby. The other 50 women will undergo lots of unnecessary worry.
I was offered the NT screening during the early portion of my pregnancy. Given my age, my child’s risk of Down Syndrome was around 1%. I was given the option to pay $200 to have the screening. If it came back negative, then I’d be worry free. If it came back positive, this would mean my child’s risk is about 1/50 or 2%.
In other words, without taking the screening, there was a 99% chance my child does not have Down Syndrome. Or, if I wanted, I could pay $200 for a test that, if positive, still means there’s a 98% chance my child does not have Down Syndrome. Is this test worth $200 to me?
As with the GDM screening, I followed my OB’s advice and had the nuchal translucency test a few months ago. The results were normal, which was comforting. The bill was around $250.
It’s tough having to juggle my emotions as a mother, my knowledge of statistics as a mathematician, and my interest in minimizing unnecessary financial expenses.